Two Span Continuous Beam With a Point and Distribution Load

Calculating bending moments and shear forces in beams – in this case 2 span continuous beams – for different loading scenarios, is probably one of the things in structural engineering that we do throughout our studies and also careers later on.

After having covered the moment and shear formulas for simply supported and cantilever beams, in this article, we'll show, the most important and easiest formulas for continuous beams due to different loading scenarios like UDL line loads and point loads.

The formulas will be supported by images showing the moment and shear force diagrams.

Now, before we get started, always remember that the unit of the bending moment is Kilonewton meter [$kNm$] and Kilonewton [$kN$] for the shear forces when in Europe.

But now, let's get started.

1. Uniformly distributed line load (UDL) – 2 Span continuous beam – formulas

Bending moment and shear force diagram | Continuous beam with 2 equal spans | Uniformly distributed line load (UDL).

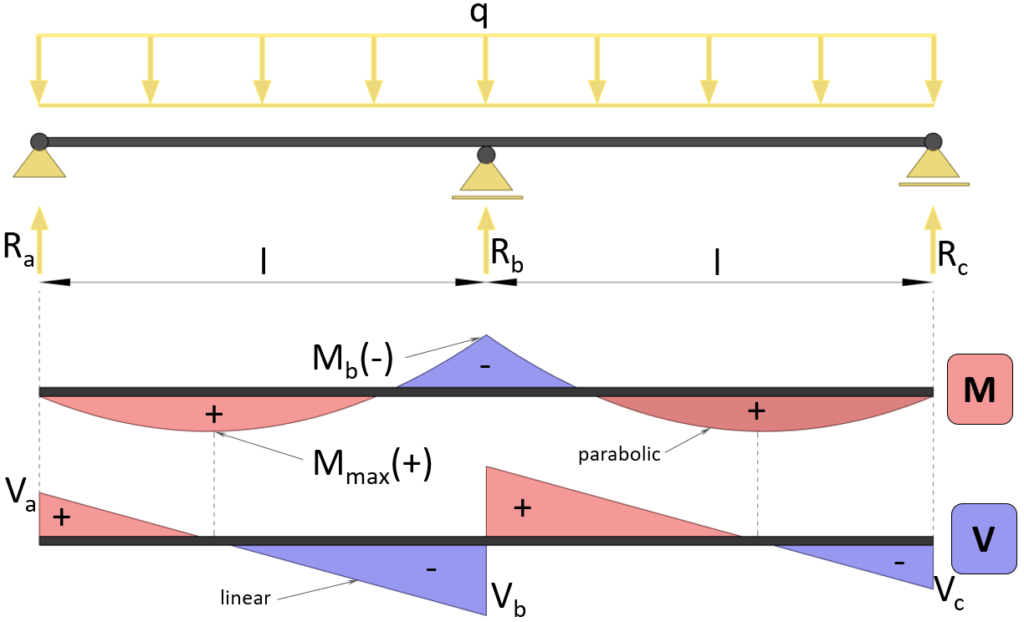
Max positive bending moment ($x=3/8 \cdot \frac{l}{2}$)

$M_{max} = 9/128 \cdot q \cdot l^2$

Max negative bending moment (at support b)

$M_{max} = -1/8 \cdot q \cdot l^2$

Shear force (at support a & c)

$V_{a} = 3/8 \cdot q \cdot  l$

Shear force (at support b)

$V_{b} = -5/8 \cdot q \cdot l$

Reaction force support a & c

$R_a = 3/8 \cdot q \cdot l$

Reaction force support b

$R_b = 5/4 \cdot q \cdot l$

2. Uniformly distributed line load (UDL) on one span – 2 Span continuous beam – formulas

Bending moment and shear force diagram | Continuous beam with 2 equal spans | Uniformly distributed line load (UDL) on one span.

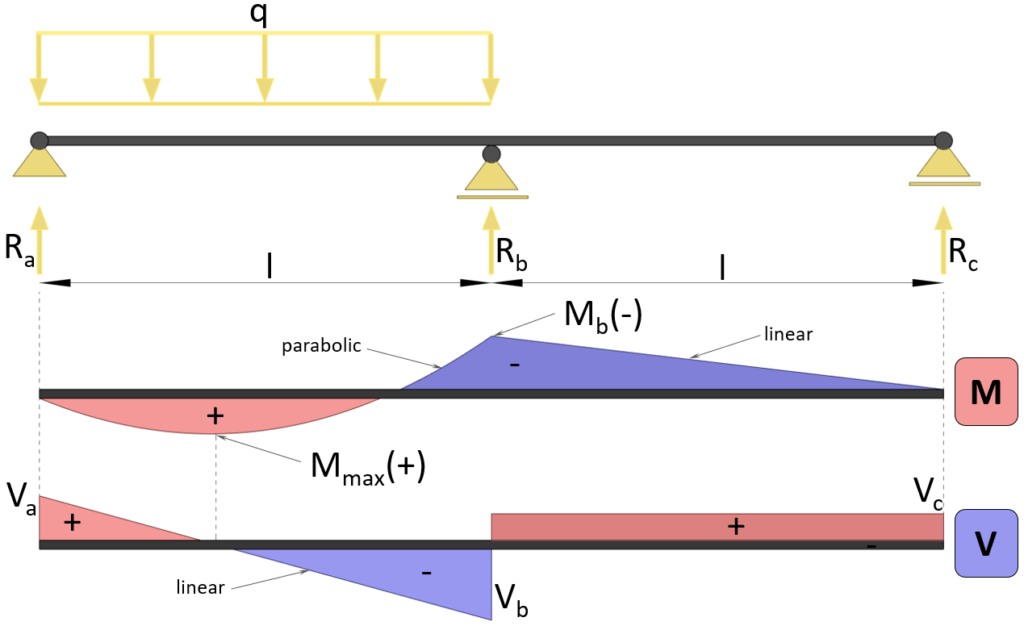
Max positive bending moment

$M_{max} = 49/512 \cdot q \cdot l^2$

Max negative bending moment (at support b)

$M_{max} = -1/16 \cdot q \cdot l^2$

Shear force (at support a)

$V_{a} = 7/16 \cdot q \cdot l$

Shear force (at support b)

$V_{b} = -9/16 \cdot q \cdot l$

Shear force (at support c)

$V_{c} = 1/16 \cdot q \cdot l$

Reaction force support a

$R_a = 7/16 \cdot q \cdot l$

Reaction force support b

$R_b = 5/4 \cdot q \cdot l$

Reaction force support c

$R_c = -1/16 \cdot q \cdot l$

3. 2 Point loads at midspans – 2 Span continuous beam – formulas

Bending moment and shear force diagram | Continuous beam with 2 equal spans | Point loads at midspans.

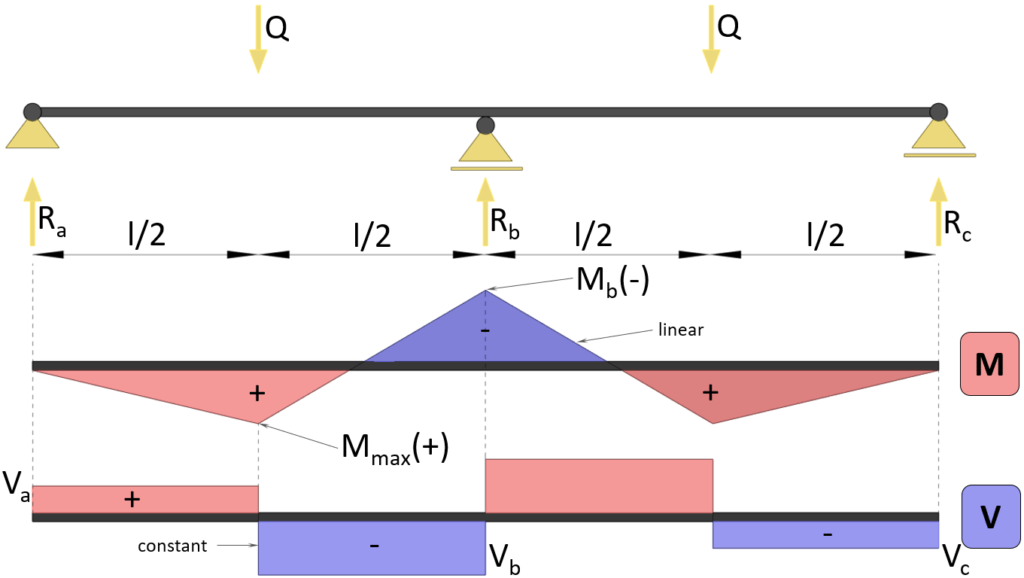
Max positive bending moment

$M_{max} = 5/32 \cdot Q \cdot l$

Max negative bending moment (at support b)

$M_{max} = -3/16 \cdot Q \cdot l$

Shear force (at support a)

$V_{a} = 5/16 \cdot Q$

Shear force (at support b)

$V_{b} = -11/16 \cdot Q$

Shear force (at support c)

$V_{c} = -5/16 \cdot Q$

Reaction force support a

$R_a = 5/16 \cdot Q$

Reaction force support b

$R_b = 11/8 \cdot Q$

Reaction force support c

$R_c = 5/16 \cdot Q$

4. Point load at midspan – 2 Span continuous beam – formulas

Bending moment and shear force diagram | Continuous beam with 2 equal spans | Point load at midspan.

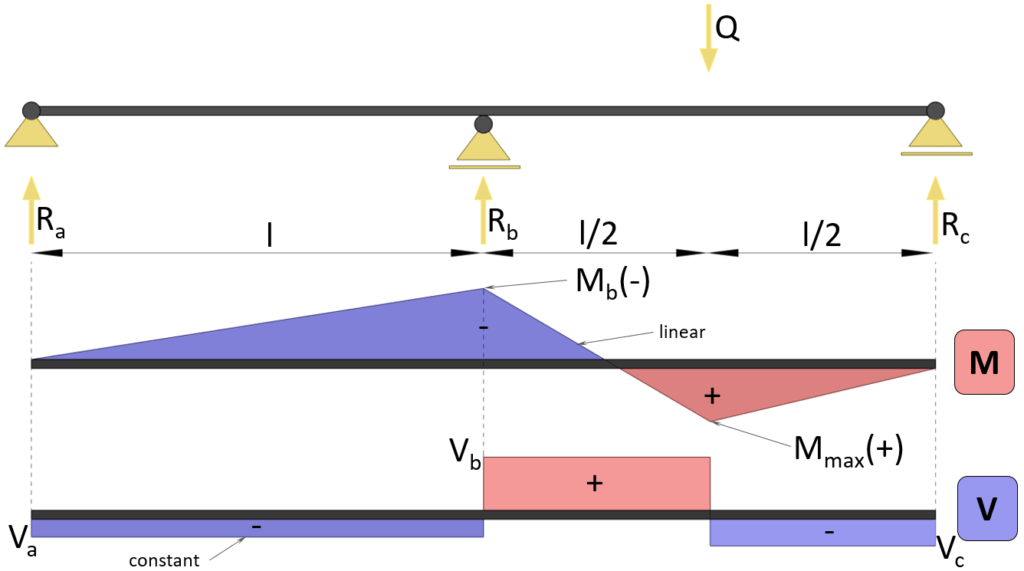
Max positive bending moment

$M_{max} = 13/64 \cdot Q \cdot l$

Max negative bending moment (at support b)

$M_{max} = -3/32 \cdot Q \cdot l$

Shear force (at support a)

$V_{a} = -3/32 \cdot Q$

Shear force (at support b)

$V_{b} = 19/32 \cdot Q$

Shear force (at support c)

$V_{c} = -13/32 \cdot Q$

Reaction force support a

$R_a = -3/32 \cdot Q$

Reaction force support b

$R_b = 11/16 \cdot Q$

Reaction force support c

$R_c = 13/32 \cdot Q$

5. Intermediate Point load – 2 Span continuous beam – formulas

Bending moment and shear force diagram | Continuous beam with 2 equal spans | Intermediate Point load.

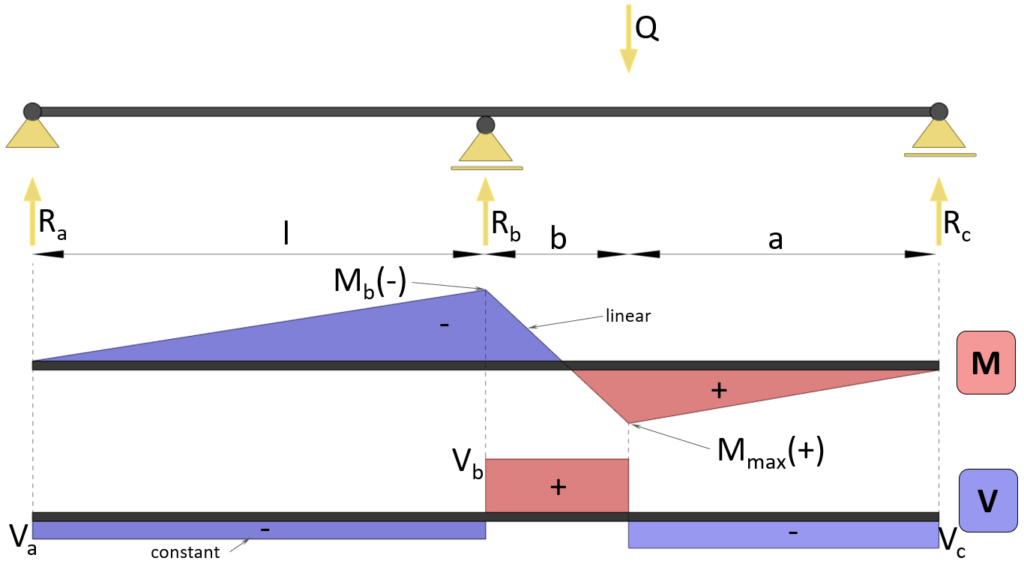
Max positive bending moment

$M_{max} = \frac{Q \cdot a \cdot b}{4 \cdot l^3} \cdot (4l^2 – a\cdot (l+a))$

Max negative bending moment (at support b)

$M_{b} = \frac{Q \cdot a \cdot b}{4 \cdot l^2} \cdot (a+l)$

Shear force (at support a)

$V_{a} = -\frac{Q \cdot b \cdot a}{4 \cdot l^3} \cdot (l + a)$

Shear force (at support b)

$V_{b} = \frac{Q \cdot a}{4 \cdot l^3} \cdot (4l^2 + b\cdot (l+a))$

Shear force (at support c)

$V_{c} = -\frac{Q \cdot b}{4 \cdot l^3} \cdot (4l^2 – a\cdot (l+a))$

Reaction force support a

$R_a = -\frac{Q \cdot b \cdot a}{4 \cdot l^3} \cdot (l + a)$

Reaction force support b

$R_b = \frac{Q \cdot a}{2 \cdot l^3} \cdot (2l^2 + b\cdot (l+a))$

Reaction force support c

$R_c = \frac{Q \cdot b}{4 \cdot l^3} \cdot (4l^2 – a\cdot (l+a))$

6. Uniformly distributed line load (UDL) – 2 unequal Span continuous beam – formulas

Bending moment and shear force diagram | Continuous beam with 2 unequal spans | Uniformly distributed line load (UDL).

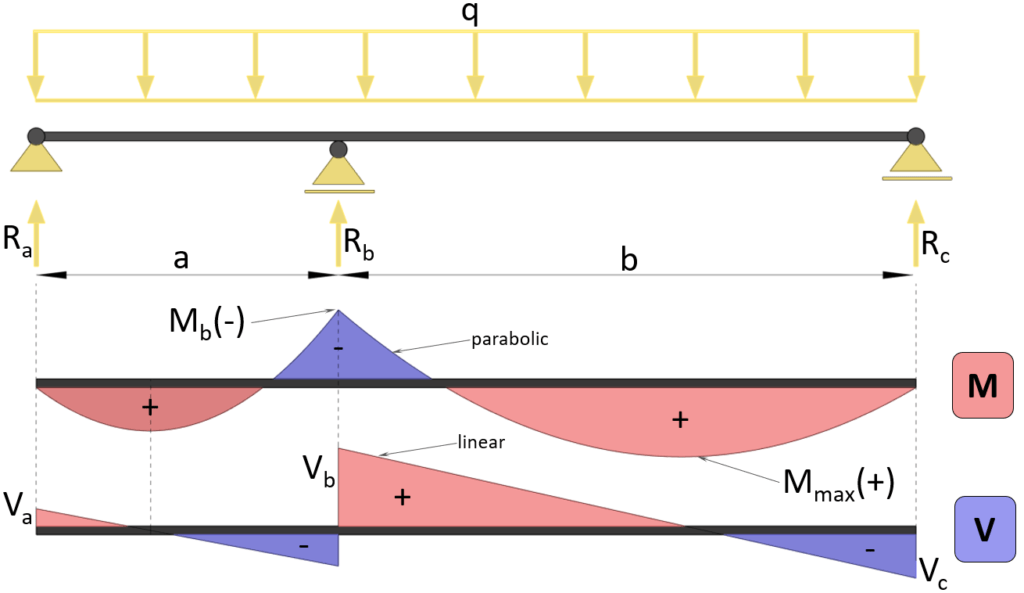
Max negative bending moment (at support b)

$M_{b} = – \frac{q \cdot a^3 + q \cdot b^3}{8 \cdot (a + b)}$

Reaction force support a

$R_a = \frac{M_b}{a} + \frac{q \cdot a}{2}$

Reaction force support c

$R_c = \frac{M_b}{b} + \frac{q \cdot b}{2}$

Reaction force support b

$R_b = q \cdot a + q \cdot b – R_a – R_c$

Max positive bending moment (between b and c)

$M_{max} = R_c \cdot \frac{R_c}{q} – \frac{q \cdot (\frac{R_c}{q})^2}{2}$

Max positive bending moment (between a and b)

$M_{max} = R_a \cdot \frac{R_a}{q} – \frac{q \cdot (\frac{R_a}{q})^2}{2}$

Shear force (at support a)

$V_{a} = R_a$

Shear force (at support b)

$V_{b} = q \cdot b – R_c$

Shear force (at support c)

$V_{c} = -R_c$

If you are new to structural design, then check out our design tutorials where you can learn how to use the calculated bending moments and shear forces to design structural elements such as

• Design of timber roof beams
• Buckling design of timber columns
• Buckling design of the collar beam

Do you miss any Moment or shear force formulas for the 2 span continuous beam that we forgot in this article? Let us know in the comments✍️

hooverhoul1980.blogspot.com

Source: https://www.structuralbasics.com/2span-continuous-beam-formulas/

Share this post